Magnetohydrodynamics

The equations of magnetohydrodynamics (MHD) describe the flow of plasma. Plasma is often refered to as the fourth state of matter next to solid, liquid and gaseous. If a gas is heated enough eventually the molecules dissociate and ionize into particles with positive and negative charges, typically ions and electrons. A plasma consists of sufficiently many negative and positive particles that exhibit collective behaviour. Most plasma situations are found in astrophysical situations, like the sun or interstellar media - in fact most of the matter in the universe is in plasma state. However, there are also many examples of plasma in natural or technological situations on earth.

Plasma Modeling

In a plasma negative and positive charges are difficult to separate globally, this makes the plasma quasi-neutral and behave similar to a gas. However, due to the charged particles a plasma flow interacts easily with electric and magnetic fields and may also create electrodynamic forces as well as electric currents. Hence, the description of plasmas requires a multi-physics approach including gas dynamics, thermodynamics of mixtures, and Maxwell equations of electrodynamics. In special situation this may be supplemented by radiative transport and turbulence models. For dilute plasmas or at low pressures, a kinetic description based on the Vlasov-Boltzmann-System is used. This system couples kinetic gas theory to electrodynamics. In astrophysics the description of plasmas may even be coupled to the Einstein equations of relativity.

The situation of a dense and fully ionized plasma allows several simplifications. While in general the plasma is described by a two-fluid-model considering ions and electrons, a single-fluid-model is sufficient in the dense and quasi-neutral case. Hence, the plasma is described by a single density, velocity and temperature like a classical gas. Still, the plasma is exposed to Lorentz-forces and its flow influences the Maxwell equations of electrodynamics. After neglecting electromagnetic waves and dissipative effects the result is the system of ideal magnetohydrodynamics for the eight fields of density, velocity, temperature and magnetic field of the plasma. For vanishing magnetic fields the system reduces to the Euler equations of gas dynamics, hence they represent a natural extension from gases to plasmas. The equations also form a hyperbolic system of conservation laws with a rich collection of magneto-acustic waves which generalize sound waves to plasma situations. Ideal MHD also allows to describe plasma shock waves in which all fields show rapid discontinuous transitions from one equilibrium state into another.

Numerical Aspects

The equations of ideal magnetoydrodynamics are typically solved on the basis of Finite-Volume methods. This requires the detailed study of the hyperbolic wave properties of the system. Ideal MHD exhibits a fast and a slow family of MHD shock waves. In both of these shocks the pressure and density increases, but the amplitude of the transverse magnetic field is increased and decreased, respectively. Besides these nonlinear wave families, there are two families of of linear waves, that is, waves that have the same speed independent of their amplitude. One familiy corresponds to the contact or tangential waves, the other represent Alfven-waves. In Alfven-waves the transverse magnetic field changes direction, while density, pressure and velocity remains unchanged. In 1970 Hannes Alfven received the Nobel Prize in Physics for his studies of MHD and the MHD waves.

The MHD system also exhibits non-classical, over-compressive shock waves in which the transverse magnetic field changes sign. These waves do not satisfy classical stability conditions and their physical and mathematical relevance is still intensively discussed. Mathematically, their formal existence leads to non-unique solutions of Riemann problems. This has considerable impact on numerical methods for MHD, where local Riemann problems on cell interfaces are the building blocks. Over-compressive wave solutions lead to strongly non-uniform convergence behaviour or pseudo-convergence for most numerical schemes. Even though this is restricted to special classes of initial conditions, these classes are rich enough to threaten numerical simulations also in the general situation.

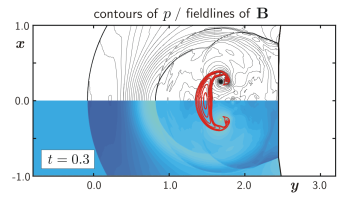
The figure above shows the flow of a gas-dynamic shock wave across a magnetized cloud with initially circular magnetic field lines. Inside the cloud the shock wave is split into different magneto-acoustic shocks, the cloud is compressed and curled up. Shear instabilities are less pronounced in comparison to a pure gas situation. This is due to the sticky behaviour of the field lines which tend to be frozen into the fluid and hinder its free motion.

Industrial Plasmas

On earth any gas discharge phenomenon, like a sparc or an electric arc, involve some sort of plasma. The most prominent example is the lightning bolt in a thunderstorm. Gas discharges come in many different variations, like low and high pressure regimes, different surface interactions, and chemical composition. plasma is used for machining in industrial applications To model these situations the system of ideal magnetohydrodynamics is often insufficient and needs to be extended by dissipative and resistive effects (real MHD) or replaced by a two-fluid or kinetic model.

The temperature inside a plasma assumes the highest values possible to observe naturally in our environment - up to 20'000K. These high temperatures are used in industrial applications like melting, drilling, and cutting. The bright flash of a gas discharge is used to provide lighting, for example, in fluorescent tubes or plasma screens. Unwanted discharges occur in electric switches and circuit breakers in which strong electric arcs can not be avoided but need to be extinguished by special technological design. Special applications involving plasma flows are electric propulsion systems for satellites and atmospheric (re-)entry flight of space vehicles. In contrast to classical gas dynamics, the computation of plasma processes remain challenging both from a numerical and modeling point of view. ACoM tries to provide fundamental applied mathematical research towards simulations of plasma flows for industrial applications.