Archive

The proposal "Simulation of Rare and Transient Events in Rarefied Gas Dynamics" (PIs: Dr. Georgii Oblapenko and Prof. Manuel Torrilhon) has been successfully funded by the German Research Foundation (DFG) and the associated project will run over the next 3 years.

The goal of the project is develop new capabilities for stochastic particle-based simulations of unsteady rarefied gas flows, with a more specific goal of being able to better model low-probability processes that despite their low incidence of occurence may be significant contributors to crucial physical effects. An example is the backscattering process in space propulsion, where even despite a low probability of particles ejected from the thruster flying in the direction of the satellite, the flux accumulates over the mission lifetime, leading to surface contamination and degradation. Modelling such low-probability phenomena is challenging, especially when 1) stochastic methods are used 2) the flow is unsteady.

Therefore, new mathematical models are needed to resolve these issues, and will be developed within the framework of the new project.

The accurate simulation of microchannel gas flows aids in the design and development of microscopic devices. One crucial aspect of theses flows is, that compared to macroscopic channel flows, gas particles travel significant distances, with respect to the width of the channel, between collisions. Hence, the relative lack of collisions is insufficient to maintain a thermal equilibrium, leading to pronounced thermal nonequilibrium effects, which the the Navier-Stokes-Fourier equations fail to reproduce. This shortcoming of classical models necessitates extended models, such as moment equations, providing higher model-accuracy at the cost of higher computational effort. Employing these models is particularly important near curved boundaries, where large local curvature of the boundary geometry induces an elevated thermal nonequilibrium as opposed to the rest of the flow.

In our recent research, we explore a model-adaptive DG scheme for a nested hierarchy of linearized moment equations. To goal is to increase computational efficiency by keeping the model as coarse as possible while increasing its complexity only in local regions of the computational domain, where the increased accuracy is required to maintain an overall target accuracy. To accomplish this, each individual element of the discretization keeps track of its model level from the model hierarchy and neighboring elements with mismatching levels are coupled by means of two half Riemann problems. The scheme is then embedded into a standard Solve–Estimate–Mark–Refine (SEMR) loop, sketched in the Figure below. Starting from an initial coarse solution, an error estimator, such as a refined solution, is used to mark elements exhibiting high error for refinement. Thereafter, the discretization is adapted and an updated solution is computed. Once the global error derived from the estimator falls below a specified tolerance, the procedure returns the final solution. By adapting only where needed, this approach significantly reduces the amount of degrees of freedom of the discretization and consequently also the time to solution. Initial results show promise and highlight future directions of improvement, such as efficient estimators and structure-preserving model-coupling.

Contact: Matthias Geratz

We have installed a new digital display in the ACOM lobby to share news and updates from our group. The screen can be used for announcements, upcoming events, job opportunities, research highlights, and similar items that may be of interest to colleagues, students, and visitors.

If you would like to show content on the display, please send it to us directly. Supported formats are JPG for images and MP4 for videos. A 1920 × 1080 landscape format is recommended to ensure good readability on the screen.

The display is also available online and can be viewed live here: https://www.acom.rwth-aachen.de/display/

5 members of ACoM took part in the 5th European Conference on Non-Equilibrium Gas Flows, which was held in Toulouse, France, from 25th to 27th of March. Eda Yılmaz presented a talk on "From 3D Tensors to 1D: A Reduction Strategy for Moment Closures in Multidimensional Systems", Dr. Satyvir Singh presented work on "Shock Wave Dynamics in Non-Equilibrium Gas Flow Regimes: Insights from Grad-Type Moment Systems", Dr. Georgii Oblapenko gave a talk on "Particle Reduction Schemes for Binning-Based Merging Approaches in Variable-Weight DSMC", visiting researcher Luke Bell presented work on "Generalized Thermodynamically Admissible 13-Moment Equations", and Prof. Torrilhon presented a talk on "A Conforming Interface Approach for Phase Transitions in Rarefied Gas Dynamics Based on the R13 Equations".

Apart from participating in the sessions, members of ACoM held many productive discussions with other members of the European non-equilibrium gas dynamics community. Dr. Georgii Oblapenko also received a prize from FLOW Matters consultancy for participating in a kinetic-theory quiz.

When gases are far from thermal equilibrium, conventional continuum models fail to accurately describe their behavior. Instead, a kinetic model that describes gases statistically is necessary so that molecular interactions can be taken into account. The Boltzmann equation is the most widely used kinetic model and is typically solved by particle Monte-Carlo methods. These methods offer high physical accuracy but are computationally expensive, especially for near-equilibrium flows, as collisions must be calculated explicitly.

An alternative kinetic model is given by the Fokker-Planck equation, which approximates the Boltzmann equation by modeling the effect of binary collisions as a drift-diffusion process. This approach allows for a more efficient particle method via the underlying Langevin equation, eliminating the need for explicit collision calculations.

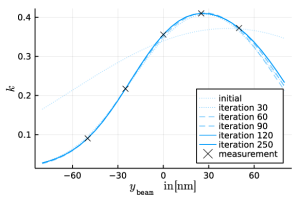
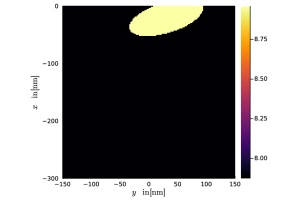
To further improve efficiency, we replace the random numbers used in the stochastic diffusion term of the velocity update with quasi-random numbers. Unlike standard pseudo-random numbers, which are scattered irregularly, quasi random number are constructed to fill the space more evenly (see first image). This reduces the statistical noise inherent in particle simulations and allows accurate results to be obtained with fewer particles (see second image).

This image shows the distribution of points in the unit square. Pseudo-random numbers are scattered irregularly, while quasi-random numbers cover the space more evenly.

This image shows the error for different moments of the distribution function (energy and stress) during relaxation from a non-equilibrium state to equilibrium. The results demonstrate that quasi-random numbers achieve faster convergence and thus require fewer particles for the same accuracy.

Contact: Lukas Netterdon

Our lab participated in the 21st International Conference for Mesoscopic Methods in Engineering and Science (ICMMES-2025), held in Wuhan, China, from July 21-25, 2025.

Dr. Baochao Shan delivered an invited talk on “Molecular kinetic modelling of surface-confined flows and three-phase interactions in nanoscale systems” and also chaired the session on “Complex fluids: multicomponent, suspension, particulate flows-2”.

Throughout the conference, Dr. Shan actively communicates with the mesoscopic method community, exchanging ideas on kinetic schemes and advanced fluid mechanics modelling approaches. The event provided a valuable platform for strengthening connections and fostering future collaborations in these areas.

Phase-transition problems pose significant challenges to the numerical method. Accurately resolving the moving domain, involving arbitrary topology changes, is one of the main problems. We develop a numerical method for phase-change problems involving rarefied gases.

In rarefied gas dynamics, classical models like Fourier's law cannot be used due to insufficient collisions and the lack of equilibrium. Extended gas dynamics models, such as moment approximations in kinetic theory, augment traditional continuum mechanics and include more variables and equations to describe the state of the gas, resulting in increased complexity of the equations. Similarly, the phase interface is subject to jump conditions that couple interface velocity, local equilibrium, and non-equilibrium variables in a possibly discontinuous way, triggering boundary layer effects that shape the bulk solution. Together with the nonlinear coupling of the evolving domain and the physical field equations, phase transitions in rarefied gas dynamics pose a significant challenge to numerical discretizations. We work on a mesh-conforming interface method based on an implicit representation of the interface, using standard finite elements and the level-set method with exact remeshing. Remeshing at every time step yields highly accurate and robust representations of the individual domain boundaries and the phase interface, allowing the interface conditions to be imposed directly and thus avoiding interpolation errors. Moreover, the field equations can be implemented without modification, using standard solvers. The finite element solver and the meshing tool in our framework are exchangeable and adaptable.

The gif shows an exemplary interface problem highlighting the robustness of the method to deal with arbitrary domain deformations. The method captures merging, separation and removal of interface segments. Furthermore, boundary contact is supported. Temperature contours are superimposed by heat flux glyphs; the interface is highlighted in white.

Preprint available at http://dx.doi.org/10.2139/ssrn.5163120

Contact: Donat Weniger

Our lab participated in the 1st International Symposium on Non-equilibrium Transport Phenomena (NETP 2025), held in Beijing from April 7-10.

Dr. Baochao Shan and Dr. Lambert Theisen engaged in lively exchanges with the international non-equilibrium transport-phenomena community.

Baochao Shan delivered “Molecular Kinetic Modelling of Nanoscale Confined Flows” and received the Young Scientist Award, while Lambert Theisen presented “Finite Element Simulations for the Linear Regularized 13-Moment Equations” and was honored with the Young Scholar Award.

Following the technical sessions, the two researchers also took the opportunity to explore the Great Wall.

Our lab participated in the SIAM Conference on Computational Science and Engineering (CSE25), held in Fort Worth, Texas from March 3rd to March 7th. We contributed to the scientific program with several presentations and discussions beyond sessions. Prof. Manuel Torrilhon, Dr. Satyvir Singh, Eda Yilmaz, Lambert Theisen, Michael Redle, Donat Weniger, Lukas Netterdon, and Daniel Doehring delivered talks on their recent research. The conference offered a valuable opportunity for exchange with the international CSE community.

The moment closure problem is a fundamental challenge in fields such as gas dynamics, radiation transport, and biology. It involves estimating higher-order moments of an unknown probability distribution from lower-order moments. The difficulty lies in finding a way to close the moment equations that ensures they are hyperbolic and accurately capture transport dynamics. Despite various methods like Grad's closure, quadrature-based approaches, and entropy-based techniques, finding a globally hyperbolic, robust, and efficient solution remains an open question.

In our recent research, we propose a new approach to the moment closure problem based on orthogonal polynomials derived from Gram matrices, referred to as the "Gramian" closure. Its properties are studied in the context of the moment closure problem arising in gas kinetic theory, for which the proposed approach is proven to have multiple attractive mathematical properties. Numerical studies are carried out for model gas particle distributions and the approach is compared to other moment closure methods, such as Grad's closure and the maximum-entropy method. The proposed ``Gramian'' closure is shown to provide very accurate results for a wide range of distribution functions.

The figure shows relative error of the next higher moment for a range velocity shifts in the bimodal test case. The left part of the figure shows the relative error for even number of moments while the right one shows odd cases. Different plot markers with colors represent the closure. Note, that the Gramian and extended Gramian closure are defined in the even and odd case differently.

ArXiv Preprint

Contact: Eda Yilmaz

Originally introduced to describe a transition region in stars, the shallow water magnetohydrodynamics (SWMHD) model is now used throughout a number of solar physics and geophysical applications. In these applications, it is common to see phenomena that result from just a small perturbation of a steady-state solution. However, if using a standard method to try and capture these numerically, one may miss these small phenomena entirely unless the grid is refined significantly. This refinement may prove quite costly, and even completely unreasonable in large 3-dimensional simulations.

Well-Balanced (WB) schemes provide one alternative solution to this issue. Such methods preserve (non-trivial) steady-states of the system to order machine precision, in turn allowing one to capture small perturbations of these steady-states on coarse meshes. To this end, we propose a WB finite volume method for both the 1-D and 2-D SWMHD system. These methods also properly treat the divergence-free condition of the magnetic field on a discrete level. The WB and divergence-free properties of the proposed schemes are both provable, and several numerical experiments demonstrate a high resolution of obtained results and a lack of spurious oscillations.

This figure presents the proposed WB method (top row) against the non-well-balanced (NWB) variation (bottom row) and their abilities (or lack thereof) to capture a small perturbation of a steady-state. It is clear that the WB method captures the proper structure of the solution even on a coarse mesh, while the NWB method has smearing of the solution due to numerical error -- even on a refined mesh.

Paper / ArXiv Preprint

Contact: Dr. Michael Redle

A large part of the ACoM team took part in the 33rd International Symposium on Rarefied Gas Dynamics in Goettingen, from 15 to 19 July 2024.

The following research was presented in the oral sessions:

1. Dr. Baochao Shan presented his work on "Kinetic Modelling of Nanoscale Heat and Mass Transfer of Confined Van der Waals Fluid"
2. Donat Weniger presented his work on "Unsteady Stefan Problem with Kinetic Interface Conditions for Rarefied Gas Deposition"
3. R.-Paul Wilhelm presented his work on "Simulation of multi-species kinetic turbulences with the Numerical Flow Iteration"
4. Dr. Milana Pavic-Colic presented her work on "Boltzmann system for a mixture of monatomic and polyatomic gases in the continuous setting" as an invited talk
5. Dr. Georgii Oblapenko presented his work on "Particle Merging Strategies for Variable-Weight DSMC Simulations"
6. Vladimir Dordic presented his work on "Finite Element Method for Polyatomic Moment Equations"
7. Dr. Satyvir Singh presented his work on "Application of regularized 13-moment equations to continuum-rarefied gas flow over aerospike blunt body"

The following research was presented during the poster sessions:

1. Eda Yilmaz presented her work on "On Nonlinear Closure for Moment Equations Based on Orthogonal Polynomials"
2. Leo Basov presented his work on "Simulation of Shock-Induced Hydrodynamic Instabilities Using Particle and Continuum Approaches"
3. Dr. Georgii Oblapenko presented his work on "High-order DG Simulations of Thermochemically Non-equilibrium Flows"

In addition, other authors from research institutions such as the Von Karman Institute (VKI), the German Aerospace Center (DLR), and the University of Sydney presented their joint work with members of the ACoM group. 

Daniel Doehring took part in JuliaCon 2024 taking place from 9th July to 13th of July in Eindhoven, NL.

The talk is entitled Towards Aerodynamic Simulations in Julia with Trixi.jl and is accompanied with a reproducibility repository that contains also the slides. Furthermore, the talk has also been recorded (although with poor visibility of the speaker) and is available on YouTube.

Daniel Doehring took part in PDESoft 2024 from July 1st to 3rd held at Cambdrige, UK.

The talk is entitled Non-intrusive Multirate Time-Integration for High-Order accurate Compressible Fluid Dynamics with Trixi.jl and was part of the Fluid Applications session. You can find the slides here.

Three members of ACoM took part in the 9th European Congress on Computational Methods in Applied Sciences and Engineering, which took place in Lisbon, Portugal, from 3 till 6 June 2024.

• Tamme Claus gave a presentation on "Applying Adjoints Twice: An Efficient Gradient Implementation for Models with Linear Structure with Applications in Reconstruction for EPMA" (abstract, slides) at the "Computational Methods for Inverse Problems" minisymposium;
• Dr. Georgii Oblapenko gave a presentation on "Approaches for distribution function inference in a gas dynamics context" (abstract) at the "Computational Kinetic Theory" minisymposium;
• Prof. Manuel Torrilhon gave a talk on "Electron Probe Microanalysis: An Inverse Problem for the Radiative Transfer Equation" (abstract), also at the "Computational Kinetic Theory" minisymposium.

Our institute is one of the co-organizer of the Karman-Conference on Sustainable Computational Science and Engineering (SCSE-25) which is scheduled for 2025. It is funded by the Exploratory Research Space of RWTH Aachen.

For more details visit the conference website: www.sustainable-cse.org.

Entropy-conservative high-order method for real gas flows

Simulation of complex multi-species reacting flows (such as those occurring in combustion processes or during spacecraft re-entry) requires modelling of the internal degrees of freedom of the constituent chemical species. At the same time, it is desirable to have numerical methods that are entropy-conservative/entropy-stable, which necessitates the development of entropy-conservative flux functions. Bringing these two requirements (the ability to model internal degrees of freedom and entropy conservation) is not trivial, as the internal energies can have very complicated dependencies on the gas state.

We propose a numerical method that works for arbitrary internal energy functions, based on linear interpolation of discretized and tabulated values of the internal degrees of freedom-related quantities (energy, specific heat, entropy). The method has been implemented in the Trixi.jl numerical framework for DG-based simulations of hyperbolic problems, and compared to results obtained via the DLR TAU code, showing excellent agreement between the two approaches.

This figure shows the pressure field for a supersonic flow around a cylinder, computed using the DLR TAU code (left) and the newly developed entropy-conservative method implemented in Trixi.jl (right).

This figure shows the temperature profiles along the stagnation line computed using the DLR TAU code and the new method.

arXiv preprint / Code repository

Contact: Dr. Georgii Oblapenko

Parabolic AMR & gmsh meshes for Trixi.jl

Over the past year, the open-source Discontinuous Galerkin (DG) code Trixi.jl has been extended to feature adaptive mesh refinement (AMR) for hyperbolic-parabolic equations such as the compressible Navier-Stokes equations.

Furthermore, existing meshes such as generated by gmsh may now be used in Trixi.jl when exported to Abaqus .inp format.

This is especially useful since high-quality mesh generation is a nontrivial, resource-consuming process. Now, it is possible to use e.g. meshes provided by the NASA Turbulence research group.

This figure shows the density contour of a developing bow-shock around the SD7003 airfoil for a Mach 2 flow. Note that the shock is resolved relatively sharp due to the adaptively refined mesh cells.

In contrast, for a simulation without AMR the shock gets diffused out:

Contact: Daniel Doehring

Reconstruction of an ellipsoidal inclusion in EPMA

EPMA (Electron Probe Microanalysis is a non-destructive technique to determine the chemical composition of material samples in the micro- to nanometer range. Based on intensity measurements of characteristic x-radiation, information about the chemical composition of the sample is obtained. The determination of the underlying chemical composition (reconstruction) constitutes an inverse problem.

In this study, we focus on reconstructing an ellipsoidal inclusion of Copper (Cu) in Iron (Fe). The goal is to reconstruct the inclusion's position, rotation, shape, and interface structure.

The provided plots show (artificially simulated) k-ratio measurements for Iron (orange) and Copper (blue). Additionally, k-ratios for materials at different iterations of the optimization (dashed and dotted lines). Only the measurements marked with black crosses are used for the optimization.

The following plots show the density of the hidden truth (the material we used to artificially simulate the measurements), and an animation of the density of the reconstructed material during the optimization.

We use a k-ratio model, that simulates electron transport using the PN-approximation of the radiative transfer equation, with a subsequent model for x-ray generation and absorption. Computing the gradient of the measurement error with respect to the material parameters represents a computational challenge.

See also: github.com/tam724/pnepma, Contact: Tamme Claus

On the shock-driven hydrodynamic instability in square and rectangular light gas bubbles

A comparative investigation of the hydrodynamic instability development on the shock-driven square and rectangular light gas bubbles is carried out numerically. In contrast to the square bubble, both horizontally and vertically aligned rectangular bubbles with different aspect ratios are taken into consideration, highlighting the impacts of aspect ratios on interface morphology, vorticity production, and bubble deformation. The results show that the aspect ratio of rectangular bubbles has a considerable impact on the evolution of interface morphology in comparison with a square bubble. In horizontal-aligned rectangular bubbles, two secondary vortex rings connected to the primary vortex ring are produced by raising the aspect ratio. While in vertical-aligned rectangular bubbles, two re-entrant jets are seen close to the top and bottom boundaries of the upstream interface with increasing aspect ratio. .png)

The baroclinic vorticity generation affects the deformation of the bubble interface and accelerates the turbulent mixing. Notably, the complexity of the vorticity field keeps growing as the aspect ratio does in horizontal-aligned rectangular bubbles, and the trends are reversed in the vertical-aligned rectangular bubbles. Further, these aspect ratio effects also lead to the different mechanisms of the interface characteristics, including the upstream and downstream distances, width, and height. Finally, the temporal evolution of spatially integrated fields, including average vorticity, vorticity production terms, and enstrophy are analyzed in depth to investigate the impact of aspect ratio on the flow structure.

Singh and Torrilhon, Physics of Fluids 35, 012117 (2023)

Contact: Dr. Satyvir Singh

A large group from ACoM participated in the 2023 SIAM Conference on Computational Science and Engineering (CSE) in Amsterdam, taking place from February 26th until March 3rd.

The Kick-Off meeting for the new research unit SNuBIC was held in Düsseldorf with the currently 20 members of the unit, including PIs, newly hired PhD candidates and Post-Docs as well as current student research assistants.